One way to significantly reduce the size of an FEA job is to utilize symmetry. But how do we do it, and when can we apply symmetry? We’ll go over all that in this blog, as well as the cases of antisymmetry, asymmetry, and axisymmetry!
When Can I Use Symmetry?
When using the term symmetry in FEA, we are referring to reflective symmetry. If the geometry and loading is the same about a mirror plane, symmetric boundaries can be applied along the mirror plane. The advantages of doing this is huge; symmetry can literally cut the size of the model in half. This intersecting pipe model is doubly symmetric about the XZ and YZ planes – by using symmetry, we were able to cut the size of the model by 75%!
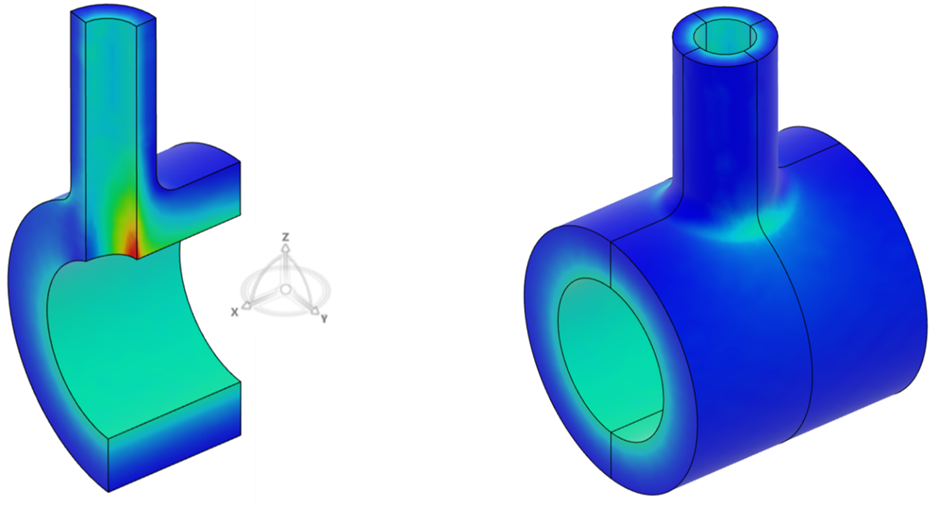
Apply Symmetric Boundary Conditions in Abaqus CAE
To apply a symmetric boundary condition along a planar face, displacements in the normal direction and rotations along the planar axes must be constrained. For example, symmetry around the YZ plane (or X-axis plane) constrains translations along X and rotations about Y and Z.
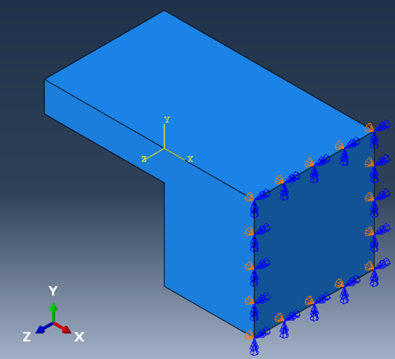
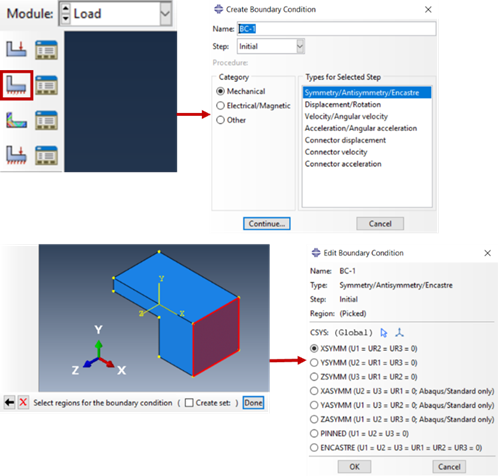
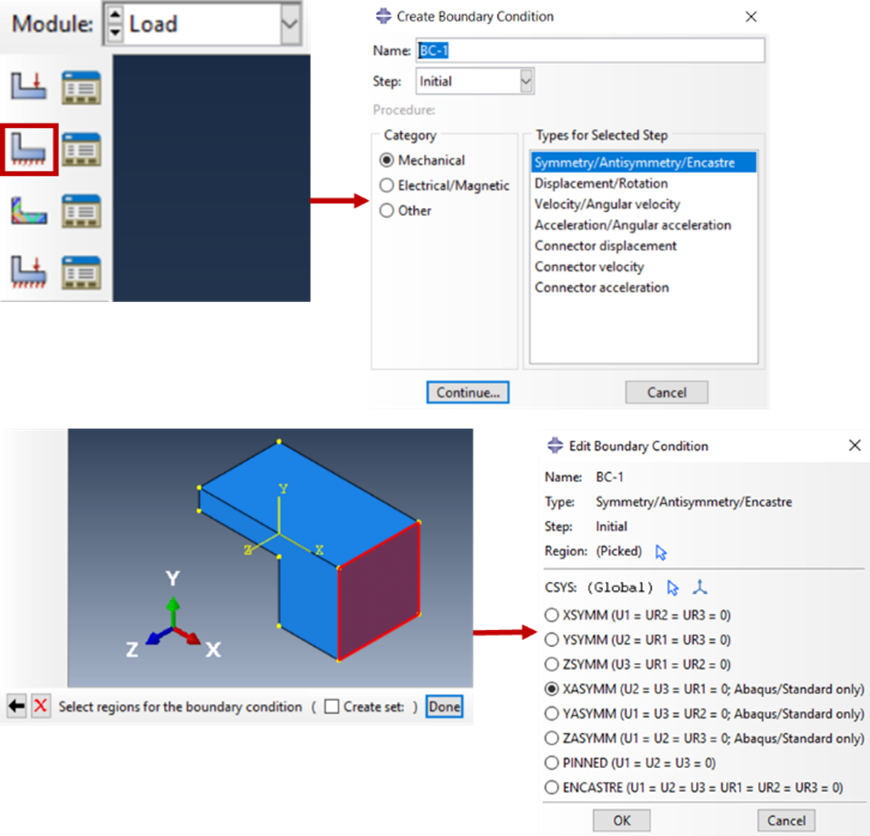
This can be done by manually constraining the required degrees of freedom; or in Abaqus CAE symmetry can be applied directly:
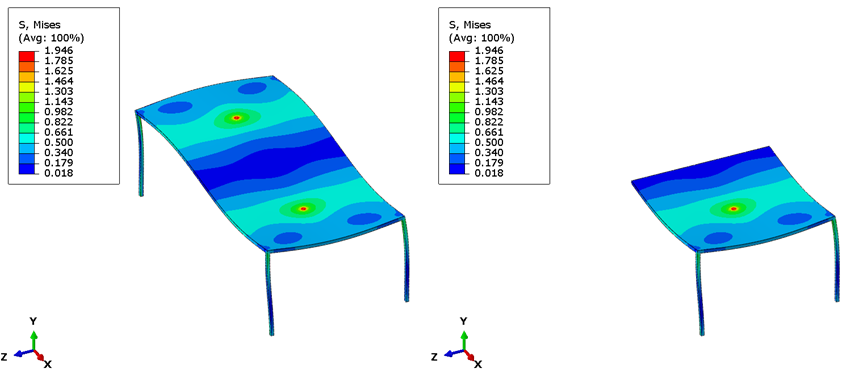
To show that this works, we’ll use a model of a table. We ran the whole table with two downward loads on the left and a half table with one downward load and symmetry on the right and the results are identical:
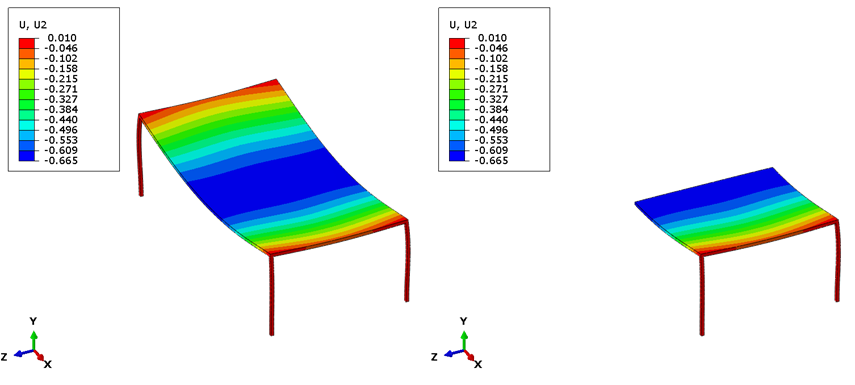
Antisymmetry
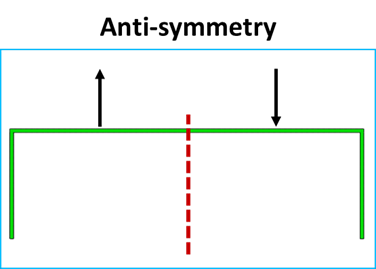
If the geometry is the same about a mirror plane, but the loading is equal and opposite about the same mirror plane, antisymmetric boundaries can be applied along the mirror plane. To apply an antisymmetric boundary condition along a planar face, rotations in the normal direction and displacements along the planar axes must be constrained. For example, antisymmetry around the YZ plane (or X-axis plane) constrains translations along Y and Z and rotations about X.
The procedure for this in Abaqus CAE is the same as for symmetry:
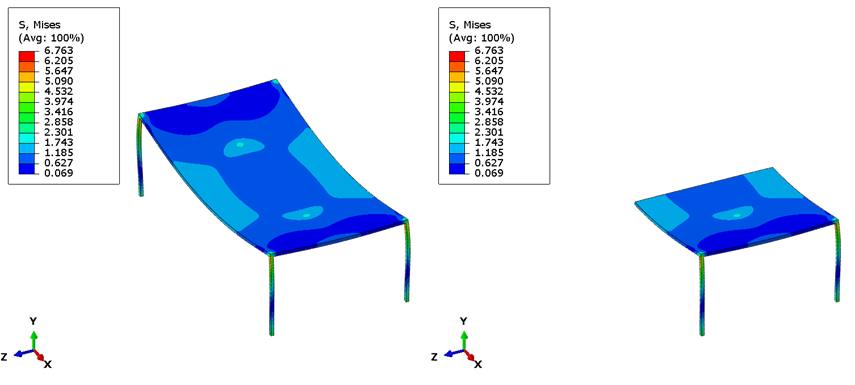
We ran the same table model with antisymmetry loading and boundary conditions below. The results between the whole and half table match, although if you think about it, this wouldn’t be very realistic for a table! Also, note that you cannot visualize the behavior of the other (non-modeled) side of the table with this method. Only the side that is modeled will be relevant, although the other side can be assumed to behave in an equal and opposite manner in a linear analysis.

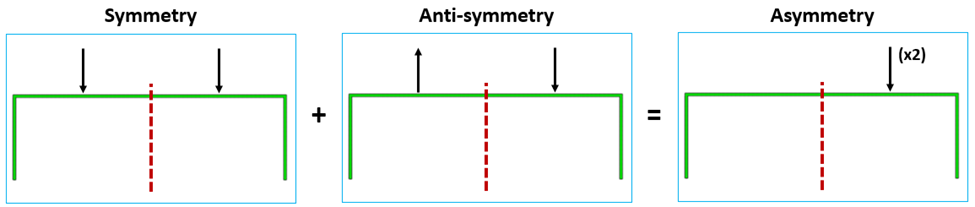
Asymmetry
One nifty property of symmetric and antisymmetric boundary conditions is that in linear analyses, the loads will cancel out if you add load cases with symmetric and antisymmetric boundaries together. This allows us to apply asymmetric loads.
To prove this out, we used the table example – a half table was ran using symmetry and antisymmetry boundary conditions and the stresses and displacements of both were added together. This was compared to a whole table with twice the load. As we can see in the images below, the results are the same.
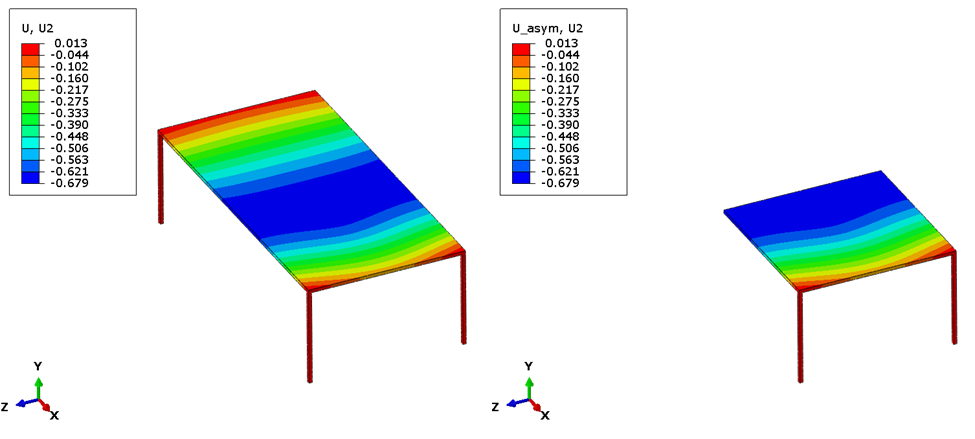
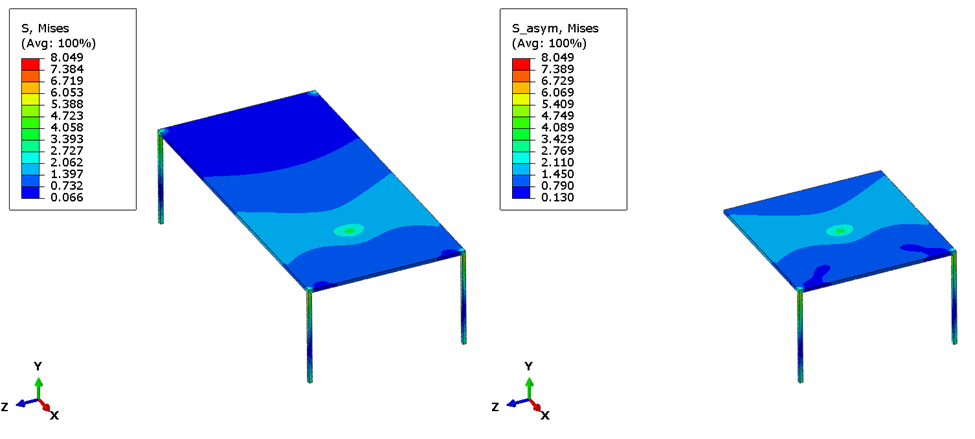
Again, note that you cannot predict the behavior of the other (non-modeled) side of the table with this method. Only the side that is modeled will be relevant – and there is no appropriate way to estimate the behavior of the other. Further, this approach won’t work if there are nonlinearities in the model.
Axisymmetry
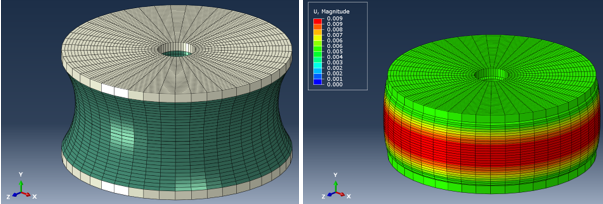
Axial symmetry (or axisymmetry for short) can be used if both the geometry and the loading can be rotated about an axis. For example, the mount shown in the picture below is axisymmetric about a center axis. However, this time, instead of a boundary condition, a special element type, the axisymmetric element, is used instead. Using them, we can model a planar cross section of the mount instead of modeling the entire mount in 3D. This simplifies the analysis significantly.

The axisymmetric elements are modeled with respect to the axis of symmetry, so no specific boundary conditions are needed in the radial direction. Symmetry about the XZ plane was applied to further simplify the model, and the pressure load was applied to the bottom of the mount.

The Abaqus element formulation is CAX, which is an axisymmetric solid element. Model features such as boundary conditions and section definitions work as if the elements are 3D, but the simulation runs in 2D.

We can use the sweep/extrude and mirror/pattern options in “ODB Display Options” to view the full shape of the mount:
ONE WORD OF CAUTION!
Symmetry should not be used in cases such as modal analyses or buckling analyses where the modes may not necessarily be symmetric.
Final Thoughts
In short, symmetry can be an excellent tool to help simplify your FEA models and reduce run time. We recommend using it whenever it’s applicable to do so.
Our expert team at Fidelis is able to help with all your sym-ulation needs. Reach out to us today!
