When we are using FEA software like Abaqus to solve a mechanical problem, we have the output in terms of displacements, stresses, strains, energies etc. To calculate the numerical values for these physical quantities, the solver has to process sets of linear and nonlinear equations in terms of degrees of freedom of the physical system. Tensors are the mathematical objects which are used to describe these physical quantities. They define multilinear relationships between sets of algebraic objects related to a vector space.
In this post we explore the mathematical foundations for the displacement and strain. This article also discusses the small strain assumptions for the Cauchy strain tensor and derivation of principal strains from the strain tensor.
Displacement
When a body is subjected to external loading, it undergoes displacement. This displacement includes rigid body translation, rigid body rotation and deformation. The deformation in a body is the relative displacement between points in it. This displacement in the theory of elasticity is continuous and differentiable. Let’s first try to understand this displacement in a deformable body in fixed cartesian system (e1, e2, e3) as shown in the figure below.
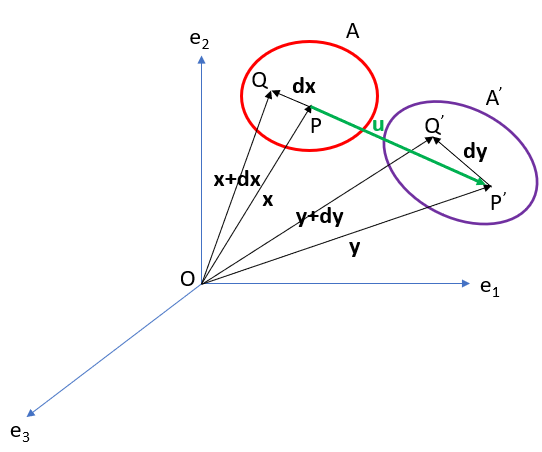
From the above figure, the initial and final configurations are defined using vectors as,

There are two ways to describe this displacement field : Lagrangian and Eulerian
-
- Lagrangian variables use initial configuration of the body A as a reference. The independent variables are x1 , x2 , x3 .
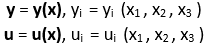
-
- Eulerian variables use the displaced configuration of the body A’ as a reference. The independent variables are y1 , y2 , y3 .
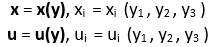
The rest of this document uses Lagrangian variables to define the body configuration.
Deformation
Deformation is defined as the relative displacement between points in a body when subjected to external loading. For the figure above, it is defined mathematically as follows:

Strain Tensors
Green Strain Tensor
So, if we have the displacement tensor above, how do we utilize that to derive strains? Well, strain is defined as the ratio of change in dimension to the original dimension of the body. This quantity is unitless and, mathematically, strain is defined from the gradient of the displacement tensor.
In cartesian coordinate system, the Green strain tensor is defined as,
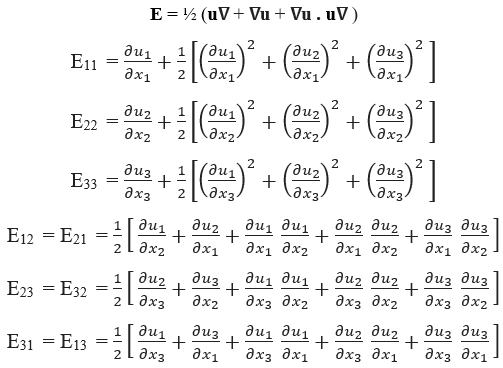
Small Strain Theory
A small strain condition can be assumed when the displacement of the body is significantly smaller than the length scale of the body. This is represented mathematically as,
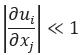
In the small strain condition, all the higher order terms in the Green strain tensor can be neglected. This yields Cauchy Strain Tensor, which is defined as,
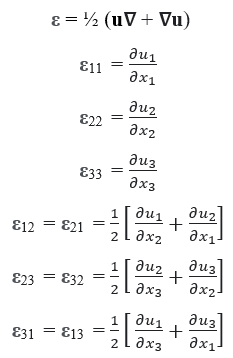
Here, the first 3 terms ε11, ε22, and ε33 are engineering normal strains and ε21, ε23, and ε13 are engineering shear strains.
Properties Of The Cauchy Strain Tensor
- It is a symmetric second order tensor.
- The transformation of strain tensor along different coordinate systems does not change the magnitude.
Principal Strain
When a body is subjected to external loading, normal and shear strains are developed. Any strain tensor (or stress tensor for that matter) with normal and shear strains can be transformed on to the principal planes, where the shear strains are zero – as shown in the figure below. These principal strains allow us to determine the objects maximum and minimum normal strain values.

The general Cauchy strain tensor is expressed as,

Determinant of the strain tensor is calculated as,

Solving for ε, we get ε1 ≤ ε2 ≤ ε3
Here,ε1 ,ε2 and ε3 are the principal strains.
The terms θ1, θ2 and θ3 are the fundamental invariants which are calculated using principal strains as follows,
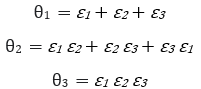
The first invariant represents the volumetric change in the system calculated using principal strains.
Final Thoughts
Hopefully this article has provided brief understanding behind the mathematical formulations for displacement, Green strain tensor, Cauchy strain tensor and principal strains.
As we’re sure you’re aware by now, we’re here to help! If you would like to learn more about simulation with SIMULIA products, or even just pick our brains on something, don’t hesitate to ,get in touch with our team!
