The popularity of CFD for industrial applications, as well as academic research to accurately predict fluid flow behavior, is ever increasing as technological advances are made in computing technology and speed (e.g., massively parallel supercomputers with GPU acceleration). Within the heart of these CFD simulations, two main methodologies exist: the Navier-Stokes approach and the Lattice Boltzmann Method (LBM). Both these methodologies are widely used in current industry practices to tackle a myriad of fluid dynamics problems and have their own set of benefits and disadvantages. In this blog, we’ll mention a brief overview of both techniques, their applications, and compare the benefits and limitations to help you understand which tools you might want to select for your next CFD simulation.
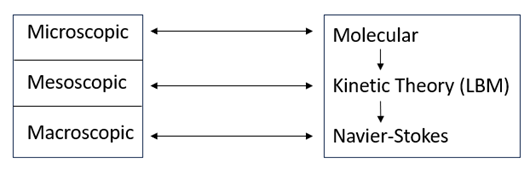
Microscopic, Mesoscopic, and Macroscopic scales
First, let’s try to understand what both these methods physically mean. We are well aware that all matter, including fluids, is composed of atoms and molecules, whose behavior can be observed on the microscopic scale, typically around nanometers. While each of these atomistic particles have unique properties, their collective behavior can be described in terms of bulk quantities such as density, velocity, and temperature. At the macroscopic scale, fluids are often treated as a continuous medium where these bulk properties are used to describe the overall behavior of the fluid. In this classical continuum approach, the fluid’s behavior is modeled using equations that predict how these quantities change over time and space, without considering the detailed behavior of individual particles.
The mesoscopic scale, situated between the microscopic and macroscopic, offers an intermediate view, where the fluid’s behavior is modeled using discrete particles on lattice structures, bridging the gap between detailed microscopic interactions and large-scale macroscopic properties. At this intermediate level, fluids are represented in terms of probability densities of finding a given particle at a given position in space and time, and with a given velocity.
The Navier-Stokes equations describe fluid properties at the macroscopic scale, i.e., in the continuum approach. The Lattice Boltzmann Method sits in the mesoscopic scale, where it connects the microscopic scale properties of fluid particles to macroscopic scales.
Navier-Stokes Equations
The Navier-Stokes equations are a set of partial differential equations that describe the behavior of fluid flow for compressible, viscous, heat conducting fluids, based on mass, momentum, and energy conservation. These describe bulk behavior of fluid quantities such as density, velocity, and temperature, using a continuum approach in the macroscopic scale. In most conventional CFD codes, these equations are solved computationally using numerical techniques such as finite difference, finite volume, or finite element methods.
The unsteady compressible Navier-Stokes equations for a Newtonian fluid can be written as follows
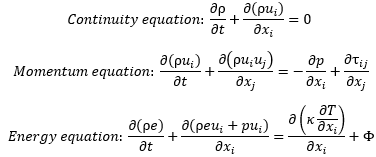
where,
p is the fluid density,
ui is the velocity component in the ith direction,
![]() is the viscous stress tensor assuming a Newtonian fluid,
is the viscous stress tensor assuming a Newtonian fluid,
e is the total energy per unit mass,
k is the thermal conductivity,
T is the temperature
and ![]() is the viscous dissipation function.
is the viscous dissipation function.
Lattice Boltzmann Method (LBM)
The Lattice Boltzmann Method (LBM) is an alternative method to mathematically describe fluid flow behavior and is becoming increasingly popular in modern CFD codes. While the Navier-Stokes equations describe fluid flow behavior at the macroscopic scale under the assumption of continuum, LBM is based on the discrete approximation of kinetic theory at the mesoscopic scale. The mesoscopic scale lies between the microscopic (atomic or molecular level) and the macroscopic scale (scales large enough that they can be observed by the naked eye, and fluid properties can be described by bulk quantities).
In LBM, the fluid domain is represented by a set of discrete lattices, and fluid properties are calculated on these discrete lattices by means of a probability distribution function. Here, a lattice is a structured grid in space, where each point on this grid, referred to as a lattice site or node, acts as a discrete location where fluid properties are computed and updated. An example of a 2D lattice is shown below, commonly referred to as the D2Q9 lattice model (2 dimensional, with 9 lattice sites).
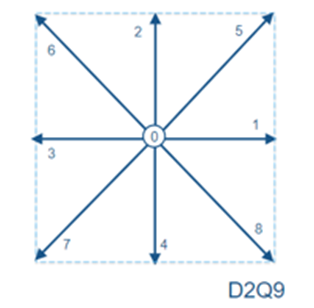
Based on this lattice structure, the solution is obtained in a 2-step process:
- Collision: Particles at each lattice node collide with each other, imparting different particle velocities to the particles, while conserving mass and momentum.
- Propagation: After collisions, the particles propagate to neighboring nodes, based on the new/updated velocities, and the new position of the fluid particles is calculated.
This collision and propagation process can be represented by the following equation:
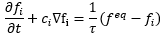
where,
fi is the discrete probability distribution function of the particle position at position i, where i = (0, 1, …, m-1), and m is the number of lattice nodes on a lattice (m = 9 on a D2Q9 lattice shown above),
c is the lattice speed,
T is the relaxation parameter.
The collision process is represented on the left side of the equation, whereas the right side represents the propagation process. These two processes form the backbone of LBM and describe how fluid particles move in a flow through the lattice structures.
Comparative Analysis between Navier-Stokes and LBM-based CFD
A brief (but non-exhaustive) summary of the comparison between the two methods is given below.
Accuracy and validation
- Navier-Stokes: High accuracy for a wide range of problems. Extensive theoretical and empirical validation has been performed and well documented in literature.
- LBM: Easier to implement and parallelize but may face challenges coupling physics such as heat transfer and turbulence modelling. Relatively newer methodology and is less validated for some applications.
Computational approach
- Navier-Stokes: Complex PDEs solved using iterative methods, which can be complex and computationally expensive
- LBM: Linear equations are solved on a lattice grid. Implementation is easier and computational time is relatively fast.
Parallelization
- Navier-Stokes: More complex to parallelize due to non-local description of flow, and careful scaling studies need to be performed to maintain proper communication and load-balancing, especially for unstructured meshes.
- LBM: Easily parallelizable due to the local description of the flow and the simple lattice structure. Highly scalable and efficient on parallel and distributed systems, including GPUs.
Computational efficiency
- Navier-Stokes: Computationally intensive, particularly for large-scale problems.
- LBM: Can be more efficient on modern hardware due to parallelization.
Complex physics
- Navier-Stokes: Complex physics require complex physical models, which can be computationally expensive.
- LBM: Since LBM captures particle interactions at the mesoscopic scale, complex physics require simpler physical models (multiphase flows, porous media, etc).
Grid generation
- Navier-Stokes: Fine scale meshes for complex geometries can be difficult and time consuming to generate.
- LBM: More straightforward to set up and modify, especially for complex geometries. Lattice grid generation is simpler since only structured meshes are employed.
Time stepping
- Navier-Stokes: Can be solved in steady or unsteady flows. Requires user to define timestep size for accurate time resolution and proper convergence.
- LBM: More straightforward to set up and modify, especially for complex geometries. Lattice grid generation is simpler since only structured meshes are employed.
Applicability
- Navier-Stokes: Widely used in classical fluid dynamics for simulating a broad range of fluid flow problems, including aerodynamics, high Mach number flows, hydrodynamics, weather modeling, etc.
- LBM: Particularly suited for problems involving complex boundary conditions, multiphase flows, and porous media. Can be challenging to simulate flows with heat transfer, high Mach number flows, etc.
Final Thoughts
In this post, we looked at the fundamental difference between Navier-Stokes and Lattice Boltzmann Method (LBM) for CFD. While Navier-Stokes solvers have traditionally been used to simulate fluid flow problems and are still widely used in the industry, LBM is gaining popularity due to its beneficial computation time, increasing accuracy, and continued fundamental research into capturing a wide range of physics.
Fidelis provides and utilizes both of these solutions in the form of Fluid Mechanics Engineer role on the 3DEXPERIENCE Platform (Navier-Stokes) and through PowerFLOW, (LBM). Don’t hesitate to reach out to our expert team to learn more!
