The Coupled Eulerian-Lagrangian (CEL) technique in Abaqus is a powerful tool to analyze the interaction between structures and fluids simultaneously without the need to use different software. In this article, we will talk about the importance and applications of CEL. But first, it’s important that we get a basic understanding
of the differences between Lagrangian and Eulerian meshing techniques, as well as their specific applications.
Lagrangian and Eulerian Meshing Techniques
The concept of Lagrangian and Eulerian meshes are demonstrated by using the following simple analogy. The average velocity of a moving train can be calculated in two ways, one way is to stay at a fixed location on the platform and record the time taken by the train to pass by. Another way is to move along with the train and record the time taken to cross fixed locations on the platform. These two approaches yield the same value of average velocity for the train. The former approach depicts the Eulerian model and the later depicts the Lagrangian.


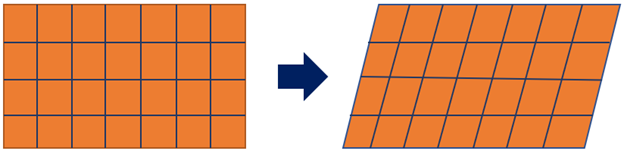
In a conventional Lagrangian model, the mesh nodes are attached to the material and deformation in the material causes mesh deformity as well. So, the material boundary will always coincide with element boundary as shown in the figure below. This formulation is simple, easy to implement and computationally less expensive.
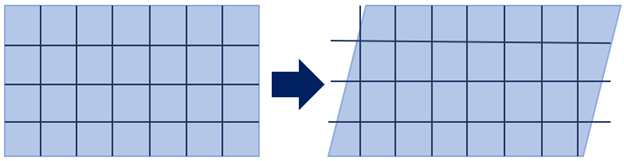
In Eulerian methods, the mesh nodes are fixed in space and material moves through the elements. Under loading, only the material deforms, and the elements remain undeformed. Because of this, the material boundary does not coincide with element boundary as shown in the figure below. As the mesh stays rigid in Eulerian analysis, element quality issues are eliminated.
Due to the ease in describing boundary conditions, the Lagrangian analysis is used to solve structural problems and contained fluid problems with small motion. However, the Lagrange model becomes unstable and loses accuracy when there is excessive deformation involved – like in riveting, blanking, and stamping processes. The computational time also increases due to frequent remeshing required to prevent the mesh from becoming overly distorted. In these circumstances, Eulerian mesh is highly efficient. It is also used in solving fluid flow and phase transformation problems where there is discontinuity in material surface across the neighboring elements.
Coupled Eulerian-Lagrangian Modelling
There are a class of problems in Engineering which require interaction between fluid and solid structures. Some examples include analyzing sloshing of fuel in a tank, deploying inflator gas in automotive air bags, wave loading on offshore structures, water flowing through dam gates etc. In these problems, we can take advantage of both meshing techniques by defining the structural part using Lagrangian mesh and fluid part using Eulerian mesh. The Eulerian-Lagrangian contact is used to define the interaction between Eulerian and Lagrangian elements. The equilibrium equations in this formulation are solved in the Eulerian framework and the transport equations of deformation gradient and Jacobian determinant are solved using the Lagragian framework. This technique is demonstrated below by simulating the fall of cup filled with water onto a hardwood floor in Abaqus.
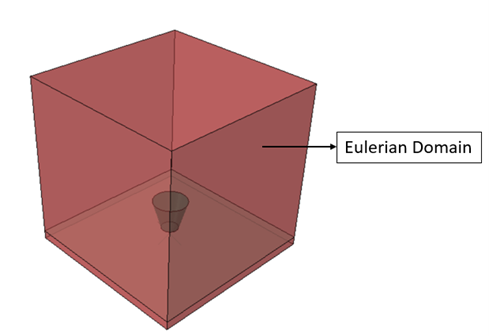
The red volume in the above figure shows the Eulerian domain. Only the glass is initially filled with water. While creating the Eulerian part, we must make sure it is large enough to account for the whole movement of the fluid during the analysis step. If the fluid moves outside of the prescribed Eulerian mesh, it disappears from the simulation. The Eulerian part is initially empty, and we use predefined material assignment to specify which materials might be filling the part over the simulation time. During the simulation, all the Eulerian mesh may not be filled with material and sometimes only some part of an element is filled with material. Abaqus stores the material flowing in each element at an instance in terms of volume fraction. Volume fraction is the percentage of element’s volume filled with material at any given instance.
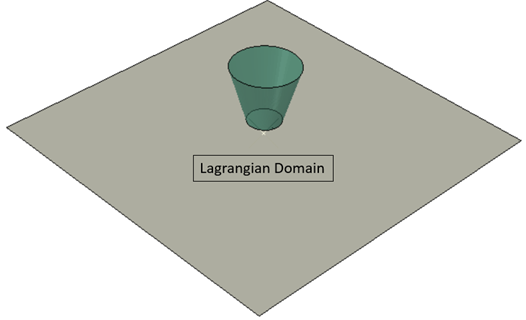
The stainless-steel cup is a deformable Lagrangian part. So, the material deformation causes mesh deformation as well and the mesh coincides with the cup boundary. The hardwood floor is a rigid part. Initial velocity is given to the cup and water, and the dynamic explicit solver is used to simulate the drop.
The animation below shows the simulation result of the effect of sloshing water in the cup when it hits the ground. This demonstrates how we can efficiently model the interaction between solid structure and fluid and simulate the fluid flow using the CEL tool in Abaqus.

Final Thoughts
Coupled Eulerian-Lagrangian method might be a term you’ve heard before while working with Abaqus, but perhaps not something that you’ve ever used? Hopefully, this article has provided you with some useful information on the CEL technique and its potency in capturing complex fluid structure interactions.
If you need help with FEA or simulation in general, don’t hesitate to give us a call! We’re passionate about what we do, and we would love to learn more about your unique engineering challenges.
